Research interests
Most of my research involves condensed matter from gases to liquids and molecular solids, such as ice and clathrates. I use a variety of theoretical tools like analytical methods of statistical physics and state-of-the-art molecular simulation algorithms. Below I give examples on some specific research areas I am interested in.
How are the various nanometric cages occupied and what is the stability domain of a mixed gas hydrate as function of pressure and temperature?
I try to derive a highly accurate equation of state for a partially ionized gas, such as the hydrogen-helium mixture in the Sun. The Screened Cluster equation of state that I'm developing with collaborators uses both analytical and numerical Path Integral Monte Carlo calculations.
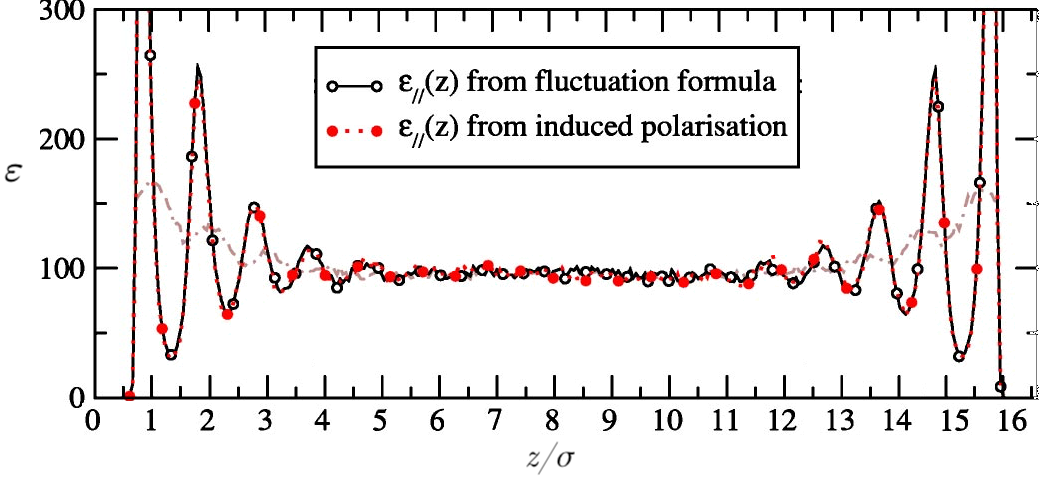
A local dielectric tensor can be introduced to characterize the local response to an electric field of a polar fluid near an interface.
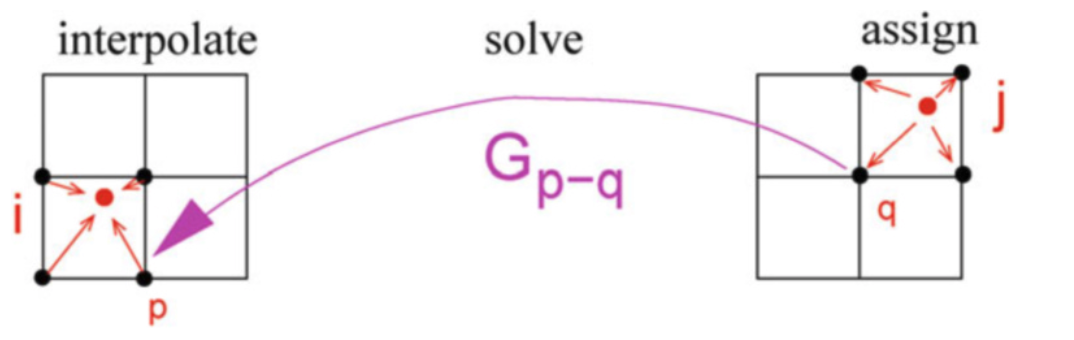
I've derived an analytical error estimate for the popular
SPME method to control easily its accuracy and to allow optimal method parameters to be determined automatically. I've generalized also the closely related P3M method to the case of dipolar forces and have shown how spurious self-forces (due to the discretization onto a grid) can be eliminated analytically.
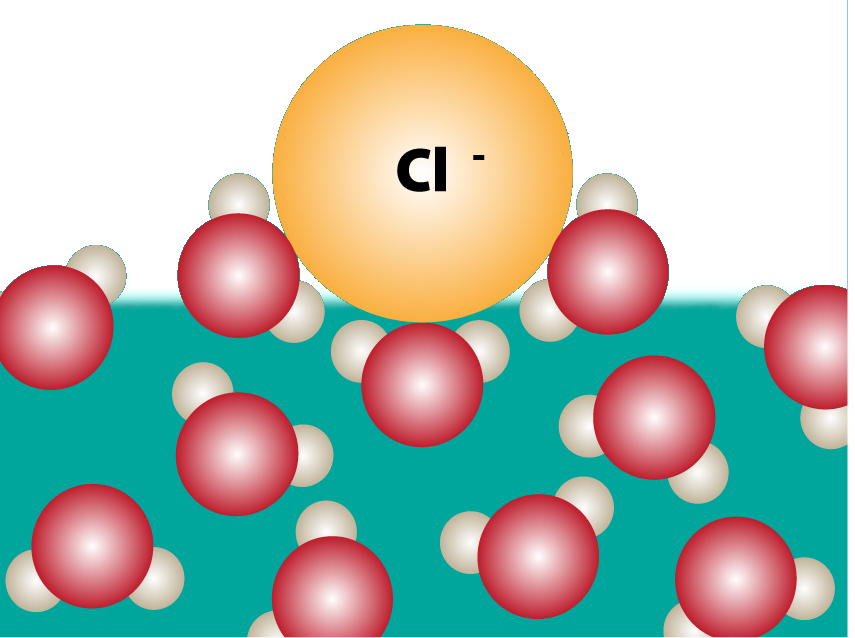
Ions near a molecular interface
To simulate a single ion near a planar interface, the standard Ewald method can be adapted to provide correct electrostatic energies and forces even though the simulation box, taken to be periodic in two directions (x-y plane), carries a net charge. How deep under the molecular surface is the dielectric discontinuity of continuum electrostatics located?
See
article 5.
Magnetic filaments, made up of nanometric beads carrying a permanent dipole moment, exhibit structural transitions when adsorbed onto an attractive surface.